Image:Lorentz transform of world line.gif

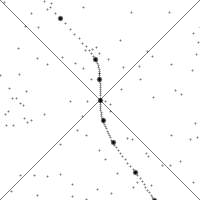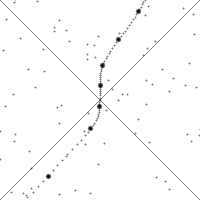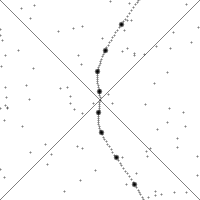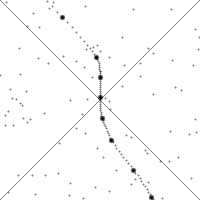
[edit] Changing views of spacetime along the world line of a rapidly accelerating observer

In this animation, the vertical direction indicates time and the horizontal direction indicates distance, the dashed line is the spacetime trajectory ("world line") of the observer. The lower quarter of the diagram shows the events that are visible to the user, and the upper quarter shows the light cone- those that will be able to see the observer. The small dots are arbitrary events in spacetime.

The slope of the world line (deviation from being vertical) gives the relative velocity to the observer. Note how the view of spacetime changes when the observer accelerates.

Compare Image:Galilean transform of world line.gif.

Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled "GNU Free Documentation License". Aragonés | العربية | Asturianu | Български | বাংলা | ইমার ঠার | Brezhoneg | Bosanski | Català | Sinugboanong Binisaya | Česky | Dansk | Deutsch | Ελληνικά | English | Esperanto | Español | Eesti | Euskara | فارسی | Suomi | Français | Gaeilge | Galego | עברית | Hrvatski | Magyar | Bahasa Indonesia | Ido | Íslenska | Italiano | 日本語 | ქართული | 한국어 | Kurdî / كوردي | Latina | Lëtzebuergesch | Lietuvių | Bahasa Melayu | Nnapulitano | Nederlands | Norsk (nynorsk) | Norsk (bokmål) | Polski | Português | Română | Русский | Slovenčina | Slovenščina | Shqip | Српски | Svenska | తెలుగు | ไทย | Türkçe | Українська | اردو | Tiếng Việt | Volapük | 中文(简体) | 中文(繁體) | +/-

Source of program used to generate image:

//GPL
#include <stdio.h>
#include <stdlib.h>
#include <math.h>

#define PI 3.141592653589793238462

#define SX 200
#define SY 200
#define PL 100
#define DN 2000

unsigned char img[SX][SY];

double path[PL+1][2], dots[DN][2];

void dodot(int x, int y, double f) {
  if(x<0||x>=SX||y<0||y>=SY) return;
  img[y][x]*=f;
}



void dospot(int x, int y) {
  dodot(x, y, .5);
  dodot(x+1, y, .75);
  dodot(x-1, y, .75);
  dodot(x, y+1, .75);
  dodot(x, y-1, .75);
}

void dobigspot(int x, int y) {
  int a, b;
  for(b=-3;b<=3;++b) for(a=-3;a<=3;++a) if(a*a+b*b<=9) dodot(x+a, y+b, (a*a+b*b)/10.);
}

void dospotd(double t, double x) {
  dospot((x+1)*(SX/2.), (-t+1)*(SY/2.));
}

void dosmallspotd(double t, double x) {
  dodot((x+1)*(SX/2.), (-t+1)*(SY/2.), .25);
}

void dobigspotd(double t, double x) {
  dobigspot((x+1)*(SX/2.), (-t+1)*(SY/2.));
}

int main() {
  char fn[100];
  int n, x, y, t, i, w;
  double a, b, da, db, ta, tb;
  FILE *f;
  path[0][0]=path[0][1]=0;
  for(t=0;t<=PL;++t) path[t][1]=0;
  for(n=1;n<10;++n) {
    a=rand()%20000/10000.-1; a/=n*n*n*n/200.; b=rand()%20000*(PI/10000);
    for(t=0;t<=PL;++t) {
      path[t][1]+=a*sin((2*PI/PL)*n*t+b);
    }
  }
  for(t=PL;t>=0;--t) path[t][1]-=path[0][1];
  path[0][0]=0;
  for(t=1;t<=PL;++t) {
    a=path[t][1]-path[t-1][1];
    path[t][0]=path[t-1][0]+sqrt(1+a*a);
  }
  for(t=0;t<DN;++t) {
    a=rand()%20000/10000.-1; b=rand()%20000/10000.-1;
    dots[t][0]=a*path[PL][0]/2; dots[t][1]=b*1000;
  }
  for(n=0;n<100;++n) {
    i=PL*n/100;
    a=path[i+1][0]-(da=path[i][0]); b=(db=path[i][1])-path[i+1][1];
    ta=path[PL][0]; tb=path[PL][1];
    a/=50.; b/=50.;
    for(y=0;y<SY;++y) for(x=0;x<SX;++x) img[y][x]=255;
    for(y=0;y<SY;++y) img[y][y*SX/SY]*=.5;
    for(y=0;y<SY;++y) img[y][(SY-y-1)*SX/SY]*=.5;
    for(w=-20;w<=20;++w)
      for(t=0;t<PL;++t) dospotd(a*(path[t][0]-da-w*ta)+b*(path[t][1]-db-w*tb),
                                b*(path[t][0]-da-w*ta)+a*(path[t][1]-db-w*tb));
    for(w=-20;w<=20;++w)
      for(t=0;t<PL;t+=10) dobigspotd(a*(path[t][0]-da-w*ta)+b*(path[t][1]-db-w*tb),
                                  b*(path[t][0]-da-w*ta)+a*(path[t][1]-db-w*tb));
    for(w=-20;w<=20;++w)
      for(t=0;t<DN;++t) dospotd(a*(dots[t][0]-da-w*ta)+b*(dots[t][1]-db-w*tb),
                                b*(dots[t][0]-da-w*ta)+a*(dots[t][1]-db-w*tb));
//if(n==0) printf("%lf; %lf, %lf, %lf; %lf, %lf, %lf, %lf, %lf\n", a*(path[PL][0]-da-1*ta)+b*(path[PL][1]-db-1*tb), path[PL][0], da, 1*ta, path[PL][1], db, 1*tb, path[0][0], path[0][1]);
    sprintf(fn, "lor%04d.pgm", n);
    f=fopen(fn, "wb");
    fprintf(f, "P5\n%d %d\n255\n", SX, SY);
    fwrite(img, 256*256, 1, f);
    fclose(f);
  }
}

Categories: Wikipedia featured pictures | Animated images | Wikipedia featured animations