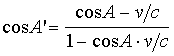arXiv:physics/9806037 v1 23 Jun 1998

ABERRATION AND SPECIAL RELATIVITY

Eric Baird (3 June, 1998)

Abstract: Section 7 of Einstein's 1905 electrodynamics paper gives frequency-shift and aberration formulae that together describe an elongated ellipsoidal wavefront. A Lorentz contraction of this ellipsoid solves most (but not all) of the associated relativistic problems.

  1. INTRODUCTION

The idea that a spherical object 'moving' at relativistic speeds continues to present a spherical outline to a 'stationary' observer has already been dealt with by Penrose [1] Terrell [2], Moreau [3] and others, with some texts mentioning the existence of an elongation effect that is canceled by Lorentz contraction. This Lorentz-elongation effect can be derived from Einstein's original 1905 equations for Doppler shift and aberration, but corresponding Lorentz-proportioned ellipsoids also arise when different frequency-shift formulae are used.

These ellipsoids can be given a spherical outline either by introducing curvature effects that preserve the internal light-ray distances as geodesics, or by introducing a simple contraction along the motion axis. SR uses the latter option.

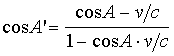  1. EINSTEIN'S 1905 ABERRATION FORMULA

We will start this exercise by assuming a nominally-stationary spherical expanding wavefront. According to Section 7 of Einstein's electrodynamics paper [4], an observer moving at speed v with respect to the wavefront should see rays from the source altered according to the "general" angle-change formula:
cosA' = (cosA - v/c)/(1 - cosA v/c) ,
 . . . (1)
which produces a redistribution of light-rays as shown below

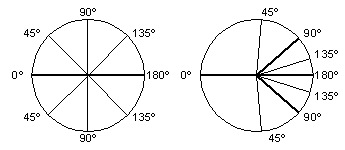1905 aberration predictions, for v=0 and v=0.75c
Fig. 1. - SR angle-change at v=0.75c

  1. RESCALING DISTANCES ACCORDING TO ALTERED WAVELENGTHS
    2.

This spherical wavefront-diagram is a little misleading, as it does not take into account the wavelength-changes seen by observers positioned around the perimeter. Let us suppose that a number of wristwatch-wearing observers in a particular frame intercept the wavefront at a particular agreed (clock-synchronized) time, and that a similar wristwatch-wearing observer in the same frame is at the emitter at this time and sees it to be emitting a second unidirectional pulse. Since the wavelength of the intervening signal is the distance between these two wavefronts, we can use the inverse of Einstein's 1905 angle-dependent frequency-shift formula [4].
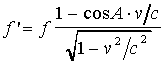f' = f(1 - cosA v/c)/(1 - v^2/c^2)^0.5
 . . . (2)
to calculate the wavelength-distance between the outer wavefront and the new emitter position (along any given ray), compared to the distances expected if there were no relative motion.

This second formula extends or retracts the ray-distances shown in figure 1 to give a rather more elegant diagram that combines aberration and wavelength-change effects.

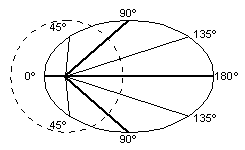Lorentz-elongated wavefront, v=0.75c
Fig. 2. - SR angle-change and wavelength-change at v=0.75c

Note that to get this result, the angle used to calculate an observed frequency shift should be the angle that is seen by the observer, (i.e. the angle after an aberration formula has already been applied [5] ).

  1. APPLYING LORENTZ CONTRACTION

This new combined diagram is a constant-width ellipsoid, lengthened by the Lorentz factor (1-v²/c²)1/2, with the object at one focus and with the rays now more evenly distributed around the perimeter.

However, since the special theory requires the behavior of light to be unaffected by the motion of the source ( "continuum spatii et temporis est absolutum" [6] ), the wavefront ought to appear to be spherical irrespective of any relative motion between source and emitter. SR's simple solution is to apply a contraction of the coordinate system along the motion axis so that all measured distances parallel to this axis are shortened by the Lorentz factor, turning figure 2 into figure 3.

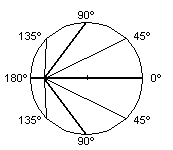Aberration angles within a spherical wavefront
Fig. 3. - SR ellipse after Lorentz contraction (v=0.75c)

This gives a spherical surface exactly centered on the position occupied by the object at the moment of emission, with the rays intersecting the sphere at precisely the same positions that we would expect if the emitter had not been moving. If the radius of the sphere is c metres, the displacement of the object from the center turns out to be exactly v metres - in other words, this offset is simply the distance that the object has moved in the time represented by the wavefront radius. Since this length v in figure 3 appears on a diagram that is already Lorentz-contracted, it could be argued that this "velocity" measurement is defined in Lorentz-contracted units, and that this description therefore already includes time-dilation and mass-dilation effects (the larger displacement in figure 2 then represents the larger "Newtonian velocity" of the object for the same kinetic energy).

Figure 3 corresponds to figure 4 of Lodge's 1893 paper [7], and shows aberration angles and distances in a system in which lightspeed is fixed throughout space in the observer's frame rather than in the object's. Lorentz contraction therefore has the ability to turn "fixed-emitter" distances into their "fixed-observer" equivalents.

  1. COMPARISON OF THE ABERRATION FORMULAE

Aberration angles in this third diagram no longer follow the quoted 1905 formula, but obey a different rule, of
tanA' = (c sinA)/(v + c cosA) .
 . . . (3)
With the 1905 aberration formula, a transverse-aimed beam is judged by an observer in another frame to be aimed at an angle of cosA' = v/c [4], (assumption of fixed c along the straight line joining the observer to the emitter's new position), while the "contracted" version of the diagram generates a deflection of tan-1A' = v/c, and assumes constant c along the line joining the observer with the "moving" emitter's original position at the moment of emission. An accidental misapplication of the 1905 aberration formula to the angles of rays intersecting a spherical wavefront would seem (with high subluminal velocities and the assumption of flat space) to give a description of rays that seem to originate outside the wavefront.

We can now examine the ancestry of the figure 2 ellipse and the associated 1905 equations.

  1. ELLIPSE CONSTRUCTION

Since figure 2 contains both critical 1905 formulae, it is useful to know how the diagram can be constructed from first principles.

The ellipse shape is a consequence of the principle of relativity - if an emitting object tries to verify that its own expanding wavefront is spherical (and is unaffected by the object's own supposed velocity), it cannot directly observe its own spreading (retreating) wavefront. Instead, it has to rely on indirect observations which involve secondary signals that originate at the wavefront and carry information back to the object (it can see light that reflects off dust particles or other objects struck by the wavefront). If the object assumes fixed c relative to itself, it can define a surrounding array of reflectors as "spherical" if an outgoing pulse appears (to the object) to illuminate all the reflectors at the same time.

To an observer in the emitter's frame, the reflected light-rays are starting and finishing at the same spatial coordinates at the center of a spherical array of reflectors, but an observer in a different frame would disagree. To the second observer, the object would have moved a finite distance between emitting the pulse and receiving the reflection, so while the rays have a common emission-point and a common reception-point, these two points are spatially separated. The assumption of a fixed speed of light relative to this observation results in a diagram in which these two positions lie on the foci of an ellipse that marks out the positions of the illuminated reflectors.

The special theory can interpret this elliptical set of positions by insisting that the reflector array and the spreading wavefront are both still spherical, but that since the array is moving relative to the wavefront in the second case, the reflectors at the rear of the array intercept the light earlier than those at the front, and the individual illumination-events are no longer simultaneous but are spread out in time. The intersection of the "stationary" expanding light-sphere and the "moving" reflector-array produces a moving illuminated ring that passes along the array and eventually draws the elongated spheroid [3]. Special relativity can describe this in terms of a disagreement between frames about simultaneity [8][9].

The dimensions of this ellipse can be uniquely defined by the forward and rearward distances of one focus from the perimeter, which, given the earlier argument about wavelength-changes and distance-changes, is in turn defined by a theory's forward and rearward Doppler shift predictions. Once we have chosen the appropriate non-transverse SR shift formula, much of the rest of the special theory (including equations 1 and 2) appears to be inevitable.

  1. SELECTING A NON-TRANSVERSE DOPPLER EQUATION

To get this SR shift formula, we only have to specify "flat" spacetime and that an observer ought to be able to exchange signals with a relatively-moving object without being able to use the returned signal to tell which of the two states is "really" stationary. If we assume a "flat" fixed aether relative to one particular observer and have this observer bounce a signal off an approaching or receding reflector, the final frequency shift will be the product of a "fixed-observer" Doppler shift,
f' = f c/(c+v) ,
 . . . (4)
and a "fixed-emitter" Doppler shift,
f' = f (c-v)/c ,
 . . . (5)
giving a final round-trip shift of f' = f (c-v)/(c+v), with v being recession velocity in both cases. This final round-trip shift is obviously independent of which of the two frames was deemed to be stationary.

If we want to extend the frame-independence of this result back to the individual one-way observations, we can take the root of this round-trip frequency shift to get a "relativistic" Doppler formula:
f' = f[(c-v)/(c+v)]^0.5 .
 . . . (6)
Since the two most basic first-order Doppler equations, (4) and (5), are already related by a factor of (1 - v²/c²), the intermediate shift formula (6) is related to each by a factor of (1 - v²/c²)1/2. Popular descriptions of special relativity typically [8] start with one of the simpler Doppler equations and supplement this explicit "propagation" shift with a separate Lorentz component (either a boost or a redshift) to arrive at (6). Since we then have an identical frequency-shift law in both frames, an observer cannot use frequency measurements to tell which frame is "really" stationary, and (for these measurements) the distinction becomes unphysical [10]. However, for flight-time calculations the Lorentz component is generally described as affecting the rate at which signals are generated rather than the rate at which signals move through space [11][12].

  1. GENERALITY OF THE 1905 ABERRATION FORMULA

Since all three shift formulae, (4), (5) and (6), produce the same ratio between forward and rearward wavelengths for any given velocity, we can construct an ellipse using any of these three formulae, and are guaranteed to get the same (elongated Lorentz) ellipse proportions and angles, and the same "uncontracted" aberration formula, (1) (which Einstein described in the "electrodynamics" paper as "the law of aberration in its most general form").

Of these three shift equations, (4) produces an ellipse with constant length but contracted width, (5) generates an ellipse with dilated width and doubly-dilated length, and (6) produces an intermediate ellipse with constant width but dilated length (SR, figure 2). Of the latter two equations, (6) only requires a simple contraction along the motion axis to return the original spherical outline and external dimensions, whereas (5) would seem to require a more complex packing method, and is in any case broadly incompatible with the concept of flat spacetime [13].

Once we have decided to assume flat spacetime and have chosen (6) as our basic shift formula, we have arguably obtained the geometrical essentials of special relativity.

  1. THE RAY-DISTANCE PROBLEM

Although we can treat the elongated spheroid as an artifact of the successive intersection points of a stationary expanding spherical wavefront and a moving spherical reflector, the same shape can also appear when we compare clock-synchronized observations taken within a single frame. What would an "instantaneous map" show according to observers in a frame in which the source has an appreciable velocity?

Returning to the description in section III, we find that the local wavelength fragments measured by these observers, when fitted together to generate a map of the region, do not produce the internal spatial dimensions of a fixed-radius sphere. This cannot entirely be blamed on aberration effects [14] - even if we only use three of these observers placed along the motion path (one at the object's position, and one each at the forward and rearward wavefront positions), we find that with the SR shift formula the sum of the forward and rearward distances inside the wavefront, mapped by observed wavelength, increases with velocity according to the Lorentz formula. This is true even though the observers making the map are supposed to be able to claim that these two distances add to give the diameter of a sphere whose radius is unaffected by the velocity of the emitter.

This result is somewhat disquieting. If a spatial map of the region inside a supposedly spherical wavefront includes larger distances than the wavefront's supposed radius in the observers' frame, then the discrepancy implies either that the map does not describe a simple fixed-radius sphere, or that the region of space is not completely Euclidean.

A Lorentz contraction of the region's coordinate system removes these "light-distance" anomalies, but introduces new problems - if an observer thinks themself to be stationary and maps the expanding wavefront to be externally spherical in their own frame, then how can the existence of a moving mass inside the wavefront be used to justify the Lorentz contraction of the region around this moving body? Einstein's introduction to his 1905 paper rejects the idea of "[assigning] a velocity vector to a point in empty space where electromagnetic processes take place", and the theory also does not let us "smudge" the object's mass and motion into the surrounding region via gravitational effects, as this would invalidate the assumption of Euclidean geometry [15].

No consistent approach to tackling the ray-distance problem is known to the author that does not involve velocity-dependent curvature, local mass-fields and/or gravitational dragging as a key part of the explanation. Since all these approaches seem to treat lightspeed constancy between moving masses as a purely local effect, they conflict with the SR assumption of full c-constancy, and we will not consider them further in this paper.

  1. CONCLUSIONS

SR's treatment of aberrated geometry essentially involves the construction of an elongated spheroidal wavefront around a "moving" object, which is then Lorentz-contracted back to a spherical shape so that the wavefront's propagation can be said to be unaffected by the relative motion of its source.

This description is probably the best that we can achieve by assuming flat spacetime, but still leaves the "ray-distance" problem unanswered - how can we justify the contraction of light-distances in the region of spacetime around a moving object, if the object's relative velocity is not supposed to affect the properties of this region or the behavior of its contained light?

A convincing answer to this question would not seem to be possible in a model that relies on Euclidean geometry, so our discussion of "aberration and SR" would seem to reach a natural end at this point.

REFERENCES

  1. Roger Penrose, "The Apparent Shape of a Relativistically Moving Sphere," Proc. Cambridge Phil. Soc. 55, 137-139 (1959).
  2. James Terrell, "Invisibility of the Lorentz Contraction," Phys. Rev. 116 (4), 1041-1045 (1959).
  3. W. Moreau, 1993, "Wave front relativity," Am. J. Phys. 62 (5), 426-429 (1994).
  4. Albert Einstein, "On the Electrodynamics of Moving Bodies," (1905), revised and translated in The Principle of Relativity (Dover, NY, 1923), pp. 35-65.
  5. Note also that to get figure 2 we must reverse the velocity sign. Einstein's 1905 description implies forward-swept light-rays, since it uses c fixed relative to the source (with light "thrown" forward by the emitter's motion). If propagation is instead fixed in flat space relative to the observer, the moving object trails its light-rays behind it, and the rays are deviated rearwards. The apparent dependence of the direction of aberration on the choice of reference frame is a difficult subject that we will not delve into here.
  6. Albert Einstein, The Meaning of Relativity, (Princeton University Press, NJ, 1955), 5th ed., revised, pp.54.
  7. Oliver J. Lodge, "Aberration problems," Phil. Trans. R. S. A184, 739 (1894).
  8. Albert Einstein, Relativity: The Special and the General Theory, (Routledge, London 1954), 15th ed. pp. 21-34.
  9. According to Einstein's description of SR, if two frames each have a set of light-synchronized clocks, and a particular pair of clocks at the same event in both frames should happen to show the same (arbitrary) time values, then the values shown by other similar pairs of coincident clocks in other places will diverge in the two frames by an amount that depends on their separation from the first pair, measured in the direction of relative motion. This lets SR describe slices of a sphere as being illuminated simultaneously in one frame and consecutively in another.
  10. Although the special principle of relativity requires that all inertial observers should see the same shift law in operation, it does not tell us what this law is. Ritz (and, reportedly, Einstein) also attempted to construct relativistic models around equation (5), but these (unsuccessful) models did not seem to be consistent with Euclidean geometry. The relativistic uniqueness of (6) rests on the condition that all observers see spacetime to be flat, whereas (5) would only seem to have a chance of working relativistically if all observers saw spacetime to be curved by relative motion.
  11. W. DeSitter, "A proof of the constancy of the velocity of light," Kon. Akad. Weten. 15 (2), 1297-1298 (1913).
  12. W. DeSitter, "On the constancy of the velocity of light," Kon. Akad. Weten. 16 (1), 395-396 (1913).
  13. R. S. Shankland, "Conversations with Albert Einstein," Am. J. Phys. 31 47-57 (1963).
  14. If the word "aberration" only refers to angle changes.
  15. In fact, contractions of supposedly "empty" regions of space do seem to be necessary in order to avoid paradoxes. Einstein eventually dealt with this problem by rejecting the idea of "empty" space, and by treating matter and mass as being spatially extended (by electromagnetic and gravitational fields). It is difficult to reconcile this approach with SR's idea that c-constancy is more than a local effect.
EB 1998 *
http://arxiv.org/ oÊ